从DCF模型谈投资 之三
2021/05/27
模型有进一步优化,文章中的细节需要改动。
模型的构建
基本面投资者最为关心的问题是公司当前值多少钱以及未来(例如两三年后)值多钱;与之相对应的是当前公司的合理估值在什么水平,未来的合理估值又在什么水平。本文中我们将从DDM出发来回答这两个问题,并引出公允价值线和公允估值线模型。这个模型可以直观的反映公允价值以及公允估值的未来走向,有助于投资者理解投资回报的来源。未来我们将在此模型的基础上对ROE、分红率以及股东要求回报率(r)等做更为细致、更为技术性的探讨。
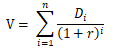
在一般的DDM中,我们假设公司为永续经营,n等于无穷。然而,在实务中,我们不可能预测无穷多年度的股利。因此,我们一般会假设公司经过一段时期的成长之后会进入一个相对稳定的状态。在稳定状态下,公司的增长率回落到很低的水平,例如1%-5%之间,甚至停止增长。由此,上面的公式变形为下面的二阶段模型:
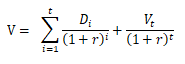
在二阶段模型中,我们需要估计1到t年中每年的股利Di,以及公司达到稳定状态时的股权价值Vt。为了具体估算Di和Vt,我们需要引入和公司经营相关的另外两个重要指标。
第一个是ROE,即净利润/净资产,这是体现公司盈利能力的最综合的指标,反映股东投入的每一块钱经过一年的时间能够产生的净回报。
第二个是分红率,即股利/净利润,该指标反映了公司每年分配多少利润给全体股东,或者说公司每年留存多少利润用于驱动未来的盈利增长,也就是公司的资本配置政策。
通俗的说,ROE反映了公司能赚多少钱,而分红率反映了公司如何使用这些赚来的钱。对于注重长期价值的基本面投资者而言,这两者都非常重要。以巴菲特为例,一方面他倾向于持有具有盈利能力(高ROE)的公司,另一方面他也要求伯克希尔的下属公司将剩余的资金返还给伯克希尔,由他自己来承担资本配置者的角色。
有了ROE和分红率,我们只要有期初的净资产,就能完成一个简单的DDM。具体而言:
当期净利润 = 期初净资产 * ROE
当期股利 = 当期净利润 * 分红率
期末净资产 = 期初净资产 + 当期净利润 – 当期股利
由此我们预测出每一期的Di。
对于稳定状态下的Vt,我们利用下面两个公式来计算:
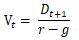
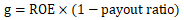
最后,我们还需要折现率r。这是一个复杂且语义很模糊的概念,我们将在未来对其进行深入考察。这里我们假设r就是投资者对于股票的要求回报率(required rate of return)。
为了便于理解,我们下面以假想的两个公司A和B作为案例来具体说明公允价值线和公允估值线模型。表一中列出了关于公司A和公司B的主要参数假设。我们先以公司A为例,假设公司在T+0年的每股净资产为10元;公司的ROE一直保持在15%;在前20年的高成长阶段,公司的分红率为30%,对应的增长率为10.5%;20年之后,公司进入稳定增长状态,此时公司的分红率为80%,对应的增长率为3%;投资者的要求回报率为10%。
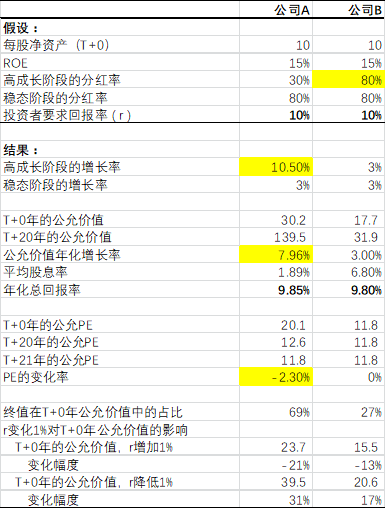
在上述假设之下,我们对前20年的股利以及终值按10%的要求回报率进行折现就能计算出T+0年公司A的每股公允价值为30.2元;类似的,我们假设时间已经推移到T+1年,我们对剩下19年的股利以及终值进行折算可以计算出当年的每股公允价值;以此类推,直至得到T+20年的每股公允价值为139.5元。如图一所示,我们连接这些公允价值点即得到随时间推移的公允价值线,它刻画了每股公允价值按年增长的路径。
同时,我们也可以在此框架下考察公允估值随时间的变化。我们以PE为例,在T+0年,当年的每股收益为期初的每股净资产乘以ROE,我们用T+0年的每股公允价值除以该每股收益即得到当年的公允PE倍数为20.1倍;其他年份以此类推。同样的,如图一所示,我们连接各年的公允PE点即得到随时间推移的公允估值线,它刻画了公允PE按年变化的路径。
对公允价值线、公允估值线的初步认识 – 以公司A为例
由图一中所示的公允价值线和公允估值线,我们可以得知在T+0年,公司A的合理股价为30.2元,对应的合理PE为20.1倍;随着时间的推移,20年后在T+20年,公司A的合理股价增长到139.5元,合理PE则回落到12.6倍。到T+21年,公司A进入稳定增长状态,合理股价的增长轨迹也进入稳定增长阶段对应的轨道,而PE则进一步回落到11.8倍,此后保持稳定。
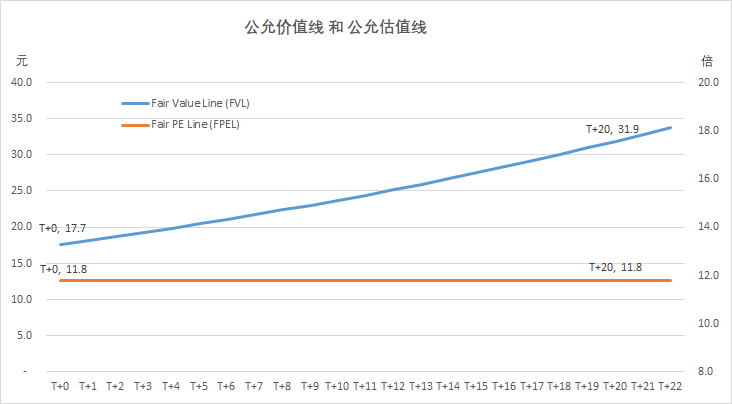
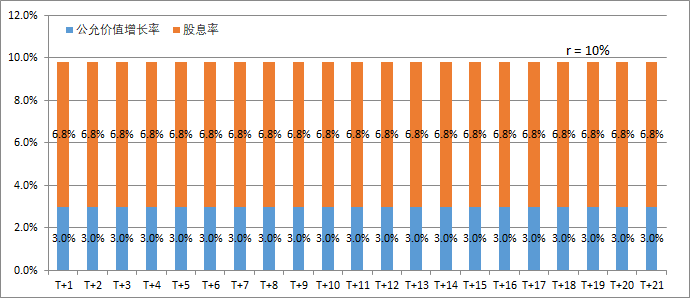
考察公司A前20年公允价值的变化,可以发现公允价值的年化增长率为7.96%,而平均股息率约为1.89%(股息率 = 当年股利/当年每股公允价值);两者之和约等于10%,即投资者的要求回报率。这个等量关系是内置于公允价值的折现计算公式中的。其含义是,如果投资者以公允价值买入某个股票,并假设投资者以公允价值卖出该股票,那么投资者的年化总回报率即为投资者的要求回报率(r),也就是计算公允价值时采用的折现率。并且,这个回报率以两种形式来实现,一种是价格(公允价值)的上涨,另一种是股息率。笔者之所以不厌其烦的一再重复这一显而易见的数学事实,是因为大量的投资者对r存在很大的误解,未来我们将就此做深入的探讨。
此外,在公司A的案例中,我们可以发现高成长阶段公允价值的年化增长率要低于利润增长率,它们之间的差值大约等于PE的变化率,即利润增长率被估值的压缩抵消了一部分,这是成长股估值中的一个普遍现象。
表一:公司A和公司B的DDM假设以及主要结果
图一:公司A的公允价值线和公允估值线
图二:公司B的公允价值线和公允估值线
图三:公司A的年化总回报率分解
图四:公司B的年化总回报率分解
对公允价值线、公允估值线的初步认识 – 公司A vs 公司B
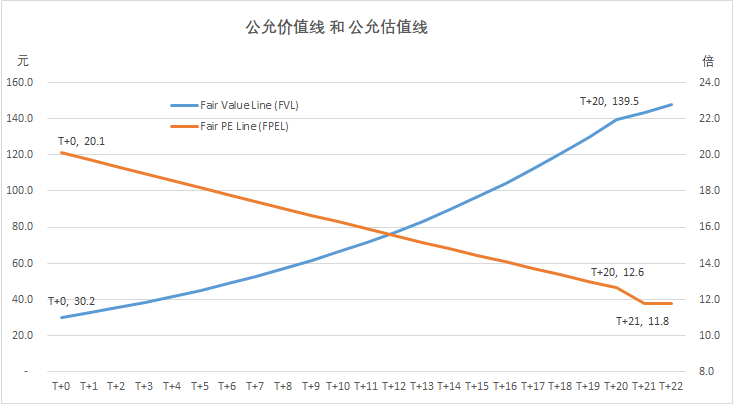
为了进一步理解公允价值线和公允估值线,我们引入公司B,用于和公司A进行对比分析。如表一所示,有关公司B的假设中仅有高成长阶段的分红率和公司A不一样,其他假设均相同。也就是说,公司B已经处于稳定增长状态,因为缺乏成长的机会,所以公司将80%的利润用于分红;而公司A则享受了20年的高成长阶段,在这20年中公司A将70%的利润留存用于增长,剩下30%用于分红。对比分析公司A和公司B,我们观察到以下结论,这些结论有些是显而易见的,有些则有点反直觉。
1、成长性的不同对两个公司的公允价值产生了巨大的影响。根据上面的假设,前20年中,公司A和公司B的增长率分别为10.5%和3%。尽管拥有同样的每股净资产和同样的ROE,公司A在T+0年的公允价值为30.2元,公司B仅有17.7元,前者是后者的1.7倍。从公允估值的角度看,在T+0年,公司A值20.1倍的PE,而公司B只值11.8倍。20年后,公司A的公允价值增长到139.5元,增长了3.6倍,年均增长7.96%;而公司B的公允价值增长到31.9元,仅增长了0.8倍,年均增长3%。此时,公司A的公允价值是公司B的3.4倍。成长性的威力由此可见一斑。
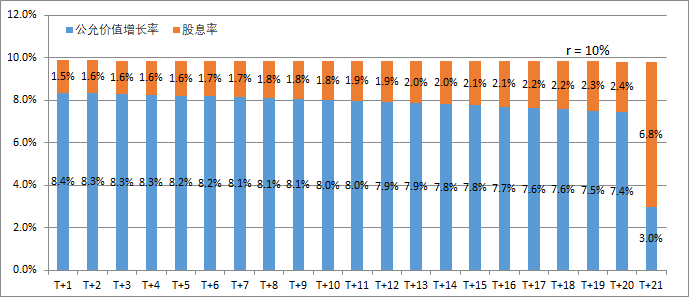
2、但是,如果在T+0时以公允价值买入公司A和B,并在T+20时以公允价值卖出,两者的年化总回报是相等的,均为10%。这是因为,公司B的年均股息收益率为6.8%,远高于公司A的1.9%。如上一节中所说,这个10%的总回报率是内置于公允价值的计算中的,只是它在不同类型公司中的体现形式有所不同。在如公司A一样的成长型公司中,它主要以公允价值增长(股价上涨)的形式体现,在公司B这样的价值型公司中,它则更多的以股息的方式体现。图三和图四分别对公司A和公司B的历年总回报进行了拆分,在T+21年,当公司A进入稳定增长状态时,它的总回报拆分就和公司B趋同了。
3、因此,只要是以公允价值买入股票,那么投资者预期的未来年化总回报就等于他在计算公允价值时采用的要求回报率r,至于这个公司是成长型公司还是价值型公司都无关紧要,因为都已经price in。同时,我们也可以推论,如果以低于公允价值的价格买入,那么获得的总回报率将高于投资的要求回报率r;反之则反是。因而,无论是投资于成长股还是价值股,买入价格都是决定未来投资回报率的最重要因素。
4、对比公司A和公司B的公允估值线,可以发现处于稳定增长状态的公司B的公允估值维持一个恒定的值,而公司A的公允估值则不断回落,直至和公司B趋同。这是因为,在高成长阶段,随着时间的推移,成长因素带来的公允价值在公司A的总价值中占比越来越少,或者通俗的说,公司A的成长性不断衰减,因此PE估值不断被压缩。在不同的成长路径下,公允估值线会呈现出不同的形态,未来我们将就此进行详细探讨。
5、在表一中,我们也考察了两个公司终值在T+0年公允价值中的占比情况。终值贡献了公司A公允价值的69%,但仅贡献了公司B公允价值的27%。这是因为公司B具有远高于公司A的股息率,因此在早期返还给股东的现金流更多(对比图三和图四的股息率部分可以获得更直观的感受),也就是说公司B的现金流的平均久期更短。因此当投资者要求的回报率r发生变化时,公司A因为久期长,它的公允价值变化幅度要远远高于公司B,即对r的敏感性更高。如果考虑到公司A的现金流久期更长,波动性更大,投资者应该对公司A要求比公司B更高的回报率,因此公司A的公允价值应该比我们现在计算出来的要低一些。具体也留到未来再做进一步讨论。