从DCF模型谈投资 之十五
20210910
本节中我们考察DCF模型中的一个重要假设,即默认再投资收益率等于投资者要求回报率r。熟悉债券的投资者会很自然的理解这个假设及其影响,因为它对应于债券投资中的再投资风险;而股票投资者往往更多的关注股价上涨带来的资本利得,对再投资风险的关注相对较少。我们将会看到,这个假设对于高分红的投资品种尤为重要,再投资收益率的高低将显著的影响到最终实现的投资回报率的高低;此外,再投资收益率和股票公允价值相对于r的弹性也是紧密相关的。
本节从两个角度出发来探讨这个问题。在Part A中,我们从现实世界的股票投资者的角度来分析,假设在期初买入1股股票,考察此后各期的再投资行为以及r的阶段性下降或上升对高股息投资品种的实际年化回报率的影响;在Part B中,我们从DDM的构建思路出发考察再投资风险以及公允价值对r的弹性,然后再将结论应用到Part A中的两个案例上。
Part A 从股票投资者的角度认识再投资风险
一、股利再投资的简单模型
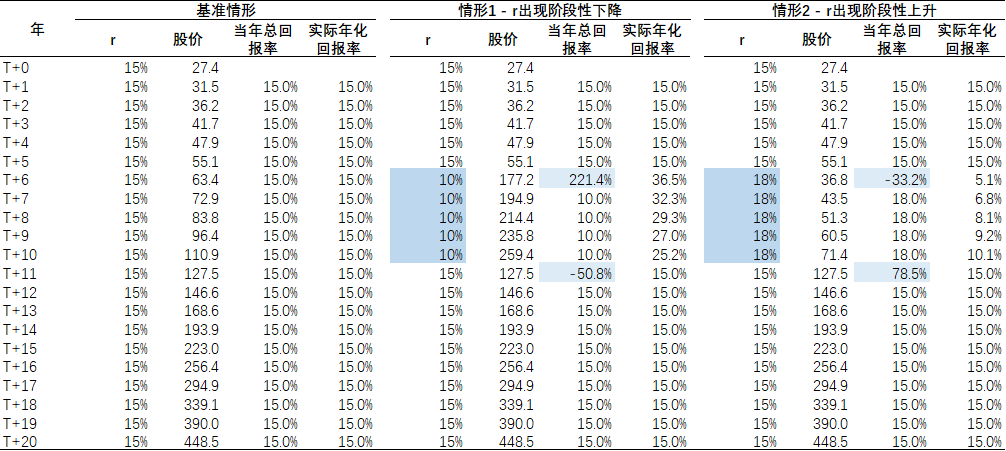
我们假设公司A的每股净资产为100元,ROE为10%;为了研究的方便,我们假设分红率为100%,即每股分红金额为10元。此外我们假设分红发生在每年的年末,投资者获得分红资金后立即全部用于买入公司A的股票作为再投资。在基准情形下,我们假设投资者的要求回报率r=15%,并保持恒定;与此相对应,公司A的公允股价为66.7元(年底分红之后)。下面我们详细考察投资者在期初买入1股公司A的股票后,该投资在此后20年间的价值增长过程。
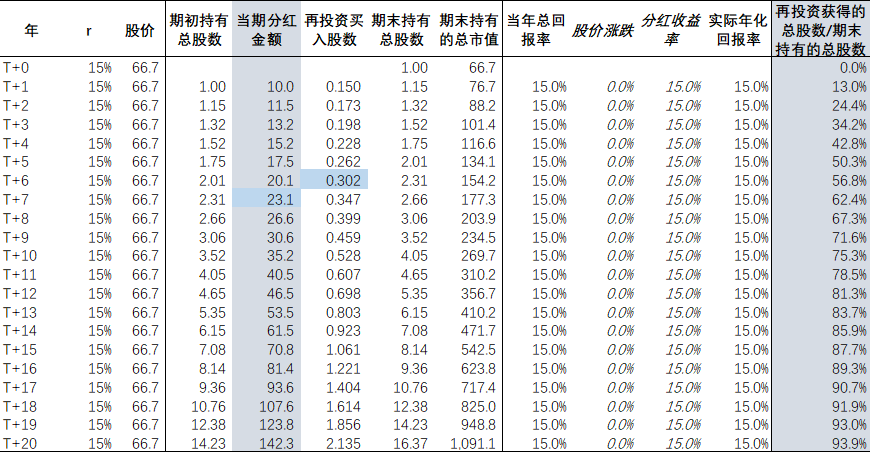
- T+0年末,投资者在以66.7元的价格买入1股公司A的股票。在T+1年末,投资者获得10元的分红,并立即以66.7的价格买入0.15股公司A的股票作为再投资。因此T+1年末的总持股数为1.15股,市值为76.7元。重复此过程,在T+20年末投资者将一共持有16.37股公司A的股票,其中通过再投资获得的股数为15.37股,占期末总股数的93.9%,而期初的那1股此时的占比仅为6.1%(也即DCF模型中的终值所占比例)。
- 或者说,投资者在T+0年末的66.7元投资到T+20年末增长到了1091.1元,这其中有66.7元来自于期初买入的那1股的价值,其他1024.4元来自于再投资(以及再投资的再投资….),由此可见再投资在高分红股票投资中的重要性。在高分红股票的投资中,复利效应主要不是通过股价的上涨来体现,而是通过股数的复利增长来体现。
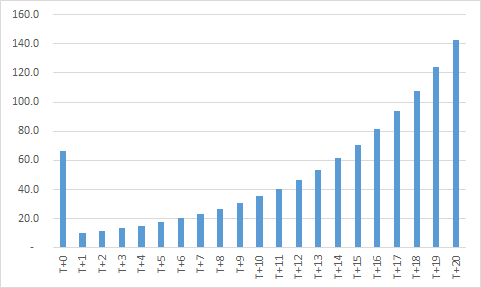
- 再投资可以看作是一种特殊形式的定投。买入高分红股票的投资者每年在收到分红后需要将其进行再次投资,因此对高分红股票的投资实际上是一系列的投资(每年的投资金额见图一),既包括了初始的第一笔买入,也包括后续每年分红后的再投资行为,这实质上就是一种定投行为。
表一:公司A – 高股息 – 基准情形
图一:公司A – 投资者每年的投资金额
二、再投资风险 – r的阶段性下降或上升对实际投资收益率的影响
DCF模型假设了后续的再投资都能获得与模型中的r相同的投资回报率,这个假设在现实世界中显然是不会成立的 ,下面我们讨论r出现阶段性变化情况下,投资者最终获得的实际年化回报率将如何变化。
情形1:r出现阶段性下降的情况
在情形1下,我们假设在T+6年,r从15%下降到10%,并持续到T+10年,此后恢复到15%,其他假设与基准情形相同。
- T+1年到T+5年,当年的总回报完全来自于分红,即15%。
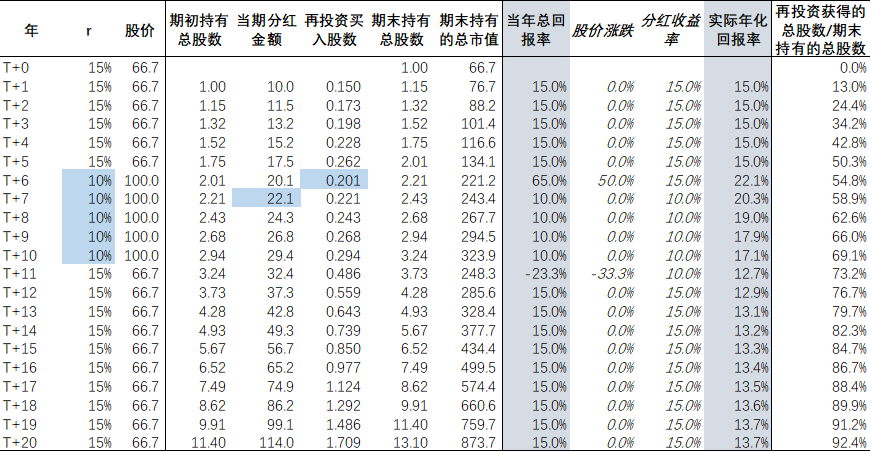
- T+6年,r的下降带来股价的上涨,当年的总回报率上升到65%。但股价的上涨导致当年的分红所得只能买到0.201股的股票,大幅低于基准情形中的0.302股。
- T+7年到T+10年,当年的总回报再次完全来自于分红,但是由于股价持续处于高位,分红收益率下降到10%的水平。此外,由于上期分红买入的股数相对于基准情形下降,因此本期的分红金额也较基准情形下降,再叠加处于高位的股价,分红能够买入的股数也就更少。简言之,这些年份的再投资收益率跟随r从15%下降到了10%。
- T+11年,r从10%恢复到15%,股价因此下跌33.3%,每股分红能够买到的股票数量得以恢复,但是因为之前5年的高股价导致T+10年末投资者的总持股数相较于基准情形有显著下降(3.24 vs 4.05),分红总额已经不能恢复到基准的水平。
- 上述影响将累积到期末,在T+20年末,投资者持有的股票总数及其对应的市值均较基准情形中低20%。投资者实际获得的年化回报率为13.7%,也显著低于基准情形下的15%。
表二:公司A – 高股息 – 情形1 – r出现阶段性下降
情形2:r出现阶段性上升的情况
在情形2下,我们假设在T+6年,从15%上升到18%,并持续到T+10年,此后恢复到15%,其他假设与基准情形相同。
- 具体的传导过程与情形1类似,不再赘述。
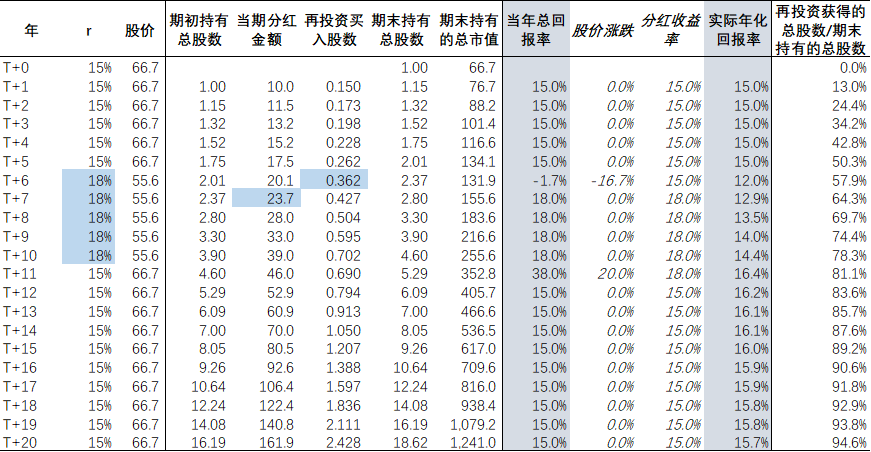
- T+6年到T+10年之间,r的上升导致股价处于低水平,因此股利再投资可以买入更多的股票,从而获得更好的再投资收益率。
- 及至T+20年,投资者持有的股票总数及其对应的市值均较基准情形下高13.7%。投资者实际获得的年化回报率为15.7%,高于基准情形下的15%。
表三:公司A – 高股息 – 情形2 – r出现阶段性上升
三、高股息 vs 零股息
公司B – 零股息案例
为了便于对比分析,我们再来考察一个零股息的案例。假设公司B每股净资产为100元,ROE同样为10%;我们进一步假设T+1到T+20年的分红率为0,每年的净利润全部由公司留存用于投资,T+21年开始分红率提高到100%。基准情形、情形1以及情形2下,r的假设均与上面公司A的案例相同。
我们采用永续增长DDM计算出公司B在T+20年末的公允股价,并将其按照各年度r的假设折现到T+0至T+19年的年末,以得出相应年份的公允股价。
我们同样假设投资者在T+0年末买入1股公司B的股票,因为公司B在前20年不分红,也就不存在股利再投资的问题,投资者的投资回报完全来自于公司股价的上涨。表四中列出了公司B在三种情形下的股价变化以及投资者的回报率。下面我们对比公司A和公司B在投资者回报率变化上的差异。
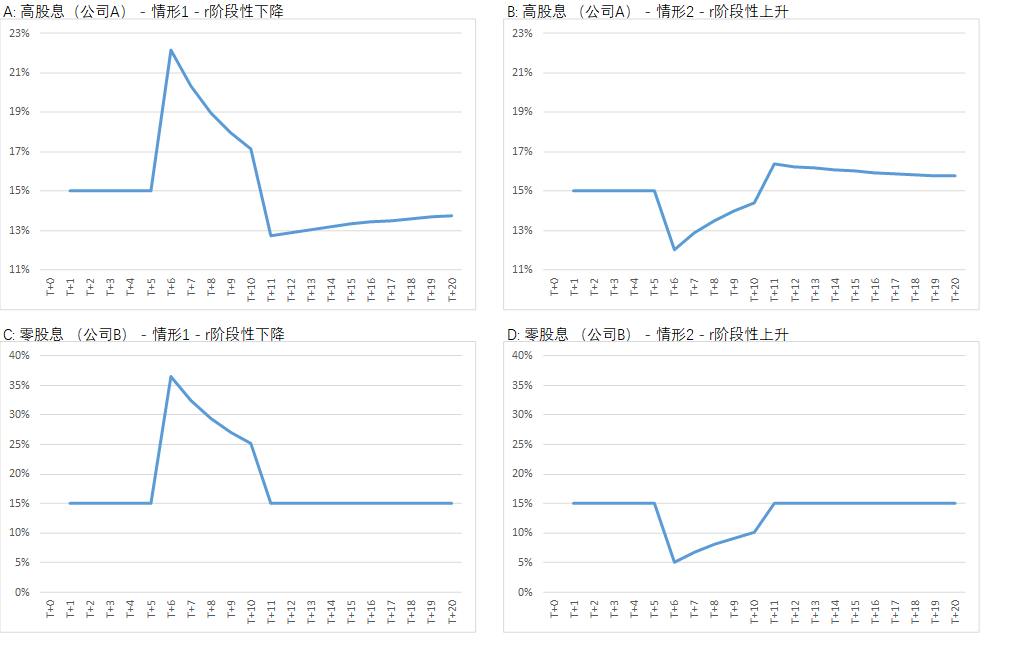
- 图二中显示了公司A和公司B在情形1(r阶段性下降)和情形2(r阶段性上升)下投资者获得的实际年化回报率的情况。这里的的实际年化回报率是指投资者持有期内的年化总回报率,例如如果投资者期初以66.7元买入了1股公司A的股票,那么在T+10年末投资者持有的总市值为323.9元,因此投资者这10年的实际年化回报率为17.1%。
- 对于高股息的投资品种(公司A),股息的再投资对实际年化回报率有重大影响:r阶段性下降会拉低此后(r恢复到期初水平后)的实际年化回报率;r阶段性上升则会拉到实际回报率。
- 对于零股息的投资品种(公司B),r的阶段性下降或上升不会对此后(r恢复到期初水平后)的实际年化回报率产生任何影响。
- 此外,显而易见,公司B的股价对r的敏感性远高于公司A。这一点我们将在Part B中进行深入讨论。
表四:公司B – 零股息 – 三种情形
图二:投资者获得的实际年化回报率
Part B 从DDM的角度考察再投资风险
一、DDM中的再投资收益率假设、实际年化回报率及久期
我们也可以沿着DDM的最基本的构建思路来理解模型对再投资收益率的假设以及再投资风险,进而考察再投资风险和久期(即公允价值对r的弹性)之间的关系。
DDM(以及所有的DCF)背后的思想实验是:投资者在T+0年投入一笔资金FV0,经过若干年,例如20年之后,这笔资金在T+20年的总价值达到TFV20;TFV20包括两个部分,第一个部分为所投资资产的公允价值变化,即从FV0变成了FV20,另一部分为持有期间获得的现金回报的再投资收益;而DDM则刻画了FV0、TFV20以及r之间的关系。在笔者所见过的教科书中,有关DDM的内容均是从折现的角度,即FV0的来源来阐述模型,例如FV0为未来各期股利和终值的现值。但这一角度掩盖了再投资收益对投资价值的贡献,也使得模型的使用者在不经意中会忽略模型对再投资收益率的假设。在后面的分析中,我们将更多的是从未来总价值(TFV20)的构成来考察DDM。在这一视角下,再投资行为的重要作用将会得到更清晰的反映。
在图三中我们从未来总价值(TFV20)出发来推导出标准的DDM,以更清晰的展开模型中包含的投资过程。A和B式中没有对再投资收益率做任何假设,可以认为是最一般的形式,即各期分红获得的再投资收益率可以各不相等;其中A1部分反映的是各期分红的再投资收益总和,A2反映的是期初投资(例如期初买入的1股股票)在T+20年末的公允价值,两者之和即为期初投资在T+20年末的总价值TFV20;将A式折现到T+0年末即得B式。在引入了各期的再投资收益率均等于投资者要求回报率这一假设之后,B式转化为C式,化简后得到D式,即标准形式的DDM形式。在标准形式下,因为对分子和分母进行了约分,D1已经不能直观的体现再投资行为;而C1尽管不是数学上的最简形式,但它更直观的刻画了各期的再投资行为。
观察C式,同时对照A和B式,我们可以有如下结论:
- C2在FV0中的占比即我们在此前各节中屡次提及的终值占比;而C1在FV0中的占比即为再投资收益的贡献度,两者之和显然等于1。因此,高股息投资品种的终值占比低也意味着再投资收益占比高,因而有着更大的再投资风险。
- C1的分子部分,即再投资收益与r同向变动;当r发生变化时,该项(再投资)的存在减缓了FV0的变化幅度。例如r上升时,未来现金流的现值下降;但(折现前的)再投资收益会上升,从而在一定程度上抵消折现率上升的影响,使得FV0对r的敏感性下降。因此,再投资风险和股价对r的弹性是一个硬币的两面,互为消长。
- 从B式也可以看到,当再投资收益率Ri高于r时,投资者最终实现的投资回报率会高于r;反之则反是。分红比率越高的标的,再投资收益率的影响越大。
图三:从未来总价值(TFV20)出发考察DDM

二、上述结论在公司A和公司B案例中的应用
下面我们以Part A中的公司A和公司B为例来说明上述结论。
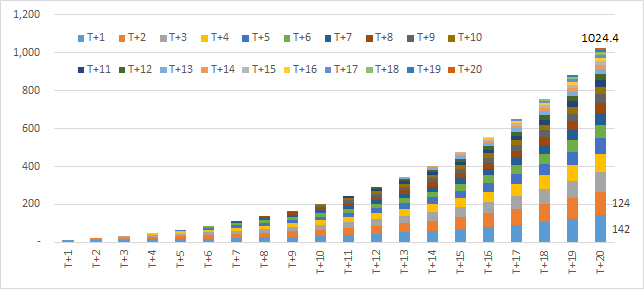
- 图四显示了基准情形下公司A累计的股利再投资收益情况,例如T+1年的10元股利在经过19年的15%的复利增长后在T+20年末达到142元,T+2年的10元股利复利增长18年后达到124元,以此类推。各年股利再投资的累计总额为1024元,在T+20年末的总价值TFV20中的占比为93.9%(表五)。由此可见再投资收益在高分红投资品种中的重要性。
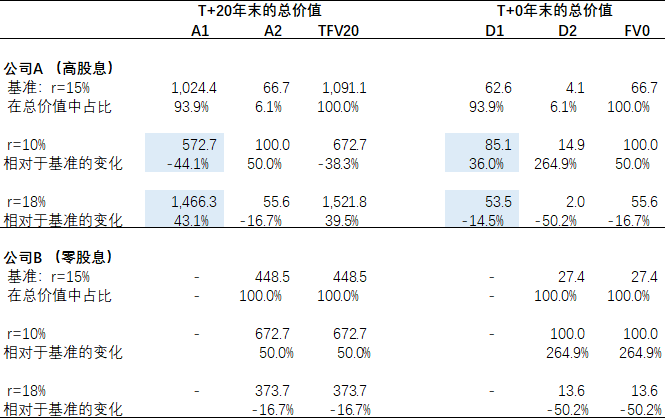
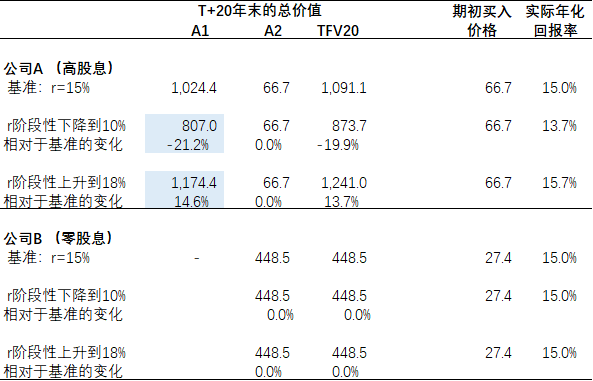
- 表五分析了公司A(高股息品种)和公司B(低股息品种)的公允价值对r的敏感性。当r从15%下降到10%时,公司A的期初公允价值(FV0)上涨50%;而公司B则上涨了265%。当r从15%上升到18%时,公司A的期初公允价值下跌了17%;公司B则下跌了50%。公司B的弹性显著高于公司A。从表五可以看出,两者在代表终值的A2(以及D2)项上的变化完全相等,弹性的差异来自于代表再投资收益的A1(以及D1)项。公司A的A1项变化和r的变化方向相同,使得D1项的变动幅度要小于D2项,从而降低了FV0的弹性。
- 表六分析了r阶段性变化对公司A和公司B实际年化回报率的影响。当r从15%阶段性下降到10%时(具体假设同Part A),公司A股票的再投资收益下降了21%,使得实际年化回报率从15%下降到13.7%;公司B因为不分红,则不受影响。r阶段性上升的情形类似,不再赘述。
- 因此股利再投资是一个双刃剑,当r上升时,再投资收益率的上升可以缓冲股价的下跌;当r下降时,再投资收益率的下降会拖累投资者实际获得的年化回报率,从而体现为再投资风险。
图四:各期股利再投资获得的复利增长
表五:公允价值对r的敏感性 – 公司A vs 公司B
表六:r的阶段性变化对实际年化回报率的影响 – 公司A vs 公司B
结论及启示
- 高股息品种的投资,复利效应主要体现在用收到的股利不断增持股票,股票数量增长的贡献远高于股票价格上涨的贡献。
- 高股息品种的投资可以类比于定投,再投资风险是投资中不可忽略的因素。
- 高股息的投资品种将未来现金流的资产配置工作交给了投资者;而成长性(低分红)投资品种的资产配置工作主要由被投资公司所承担。对投资者而言,高股息投资品种是一个累活。
- 对于长期投资者而言,股价的阶段性下跌(r阶段性上升)有利于提高高股息品种的实际年化回报率;反之则反是。
- 再投资风险和股价相对于r的弹性是一个硬币的两面,互为消长。当r上升时,再投资收益率的上升可以缓冲股价的下跌;当r下降时,再投资收益率的下降会拖累投资者实际获得的年化回报率,从而体现为再投资风险。
- 本节中,基准情形下的r被设定在了15%这一高位,因为笔者试图回答高股息的品种能否给投资者带来高水平的长期年化回报。通过本文的分析,笔者倾向于认为答案是否定的。对于个人要求回报率(例如15%)显著高于市场要求回报率(例如10%)的投资者而言,高股息投资可能不是一个很好的长期投资品种。这是因为股价通常不会长时间(例如数年)的处于低位(r处于15%甚至更高的水平),这将导致股利再投资的收益率会显著低于个人的要求回报率,从而使得最终实现的实际年化回报率低于个人要求回报率。
- 高股息品种的优势可能在于股价波动率相对较低,风险调整后的收益可能会更为理想。